6.8 Metóda „red herring“

    Pri uplatňovaní kritického myslenia sa od žiakov očakáva, aby boli aktívnymi účastníkmi vyučovacieho procesu, aby sa aktívne zapájali do aktivít na hodine. Mali by byť schopní správne argumentovať a formulovať výsledky práce na hodine, prípadné rozpory s predpokladmi vhodne korigovať. Nie je postačujúce novú informáciu získať, musia ju vyhodnotiť a zvážiť, či je získaná informácia korektná. Uvádzame charakteristiku metódy a príklad aktivity od Vanyovej a Pišúta (2014).
    Vhodnou metódou pre riešenie problémov uvedeného typu je metóda „red herring problem“. S týmto pojmom sa častejšie stretávame v literatúre, pri písaní detektívnych príbehov, kde autor čitateľa zvedie zámerne nastrčenou falošnou stopou. Príbehy „red herring“ sú konštruované tak, aby čitateľ pozorne čítal príbeh a dedukciou a vhodnou argumentáciou našiel riešenie problému. So žiakmi je možné v tomto rozmere riešiť krimi príbehy s fyzikálnou tematikou (Veselý, 2005).
    „Red herring problémy“ neponúkajú vytvoriť záver jednoduchým zhodnotením problému. Nevedú priamo k riešeniu problému, ale divergujú k záverom, o ktorých je potrebné rozhodnúť, či sú alebo nie sú relevantné. Podľa Mayfielda (2014) termín „red herring“ vznikol v časoch, kedy utečenci z väznice podhodili psom, ktorí ich sledovali, červené slede (v prekl. red herrings), aby zápach sleďov prekryl pach stopy, ktorú sledovali psi.
    Metódu „red herring“ predstavíme na aktivite, ktorá je určená žiakom 6. ročníka. Pri vyhodnocovaní meraní na ZŠ žiaci často skĺznu k výroku: „Nepresnosti vo výsledku boli spôsobené nepresným odčitovaním hodnôt na meradlách.“ V tejto aktivite by si žiak mal uvedomiť, že chybná môže byť aj metóda merania.
    
Hustota ryže
    Metódu „red herring problem“ je možné aplikovať aj na praktické činnosti žiakov na hodinách fyziky. Uvedieme príklad aktivity, ktorá nesie znaky „red herring problému“.
    Na hodinách fyziky v 6. ročníku na základných školách resp. v 1. ročníku osemročných gymnázií žiaci skúmajú ako sa správajú telesá v kvapalinách (Lapitková, 2010, s. 86). Mali by získať vedomosť, že telesá, ktoré sa vo vode potopia, musia mať hustotu väčšiu, ako je hustota vody, t.j. väčšiu ako 1 g/cm3 a telesá, ktoré plávajú vo vode musia mať hustotu menšiu ako je hustota vody, t.j. 1 g/cm3. Aktivita, ktorá môže preveriť upevnenie tejto vedomosti a súčasne rozvíja experimentálnu činnosť u žiakov, je meranie hustoty ryže. Predpokladáme (zo skúsenosti), že hustota ryže je väčšia ako 1 g/cm3, lebo, ak ju nasypeme do vody, ryža klesne na dno nádoby. Pre zistenie hustoty ryže je potrebné ryžu odvážiť a zmerať jej objem. Žiakom pripravíme odmerné valce, ryžu a váhy ako potrebné pomôcky, tým sa ich pokúsime zviesť na falošnú stopu. Žiaci spravidla odmerajú objem ryže „na sucho“ tak, že ju nasypú do odmerného valca. Ak by niektorí chceli merať objem ryže „na mokro“, učiteľ môže presvedčiť žiakov, aby meral objem „na sucho“ s odôvodnením, že ryžu bude možné znovu použiť. Opäť sa snažíme žiaka zviesť na falošnú stopu. Po nameraní dvojíc hmotnosti ryže a objemu ryže a vynesení závislosti hmotnosti od objemu ryže do grafov, určí sa hustota ryže „na sucho“ (obrázok 6.20).
    

                

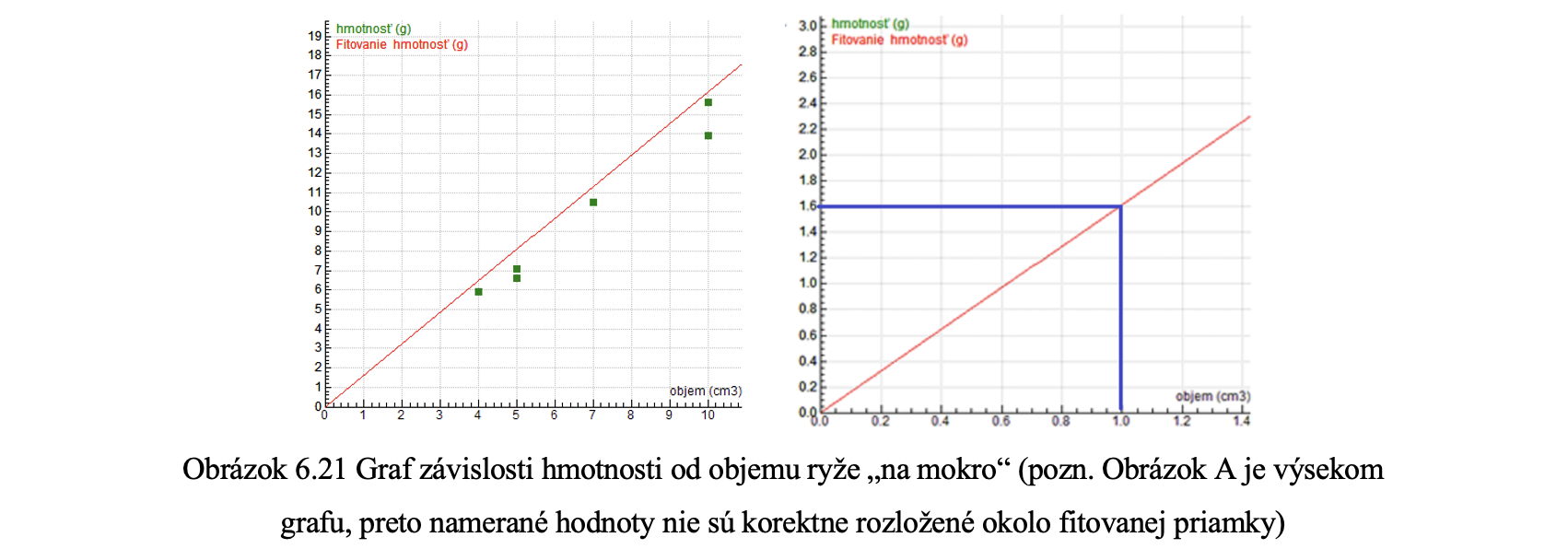
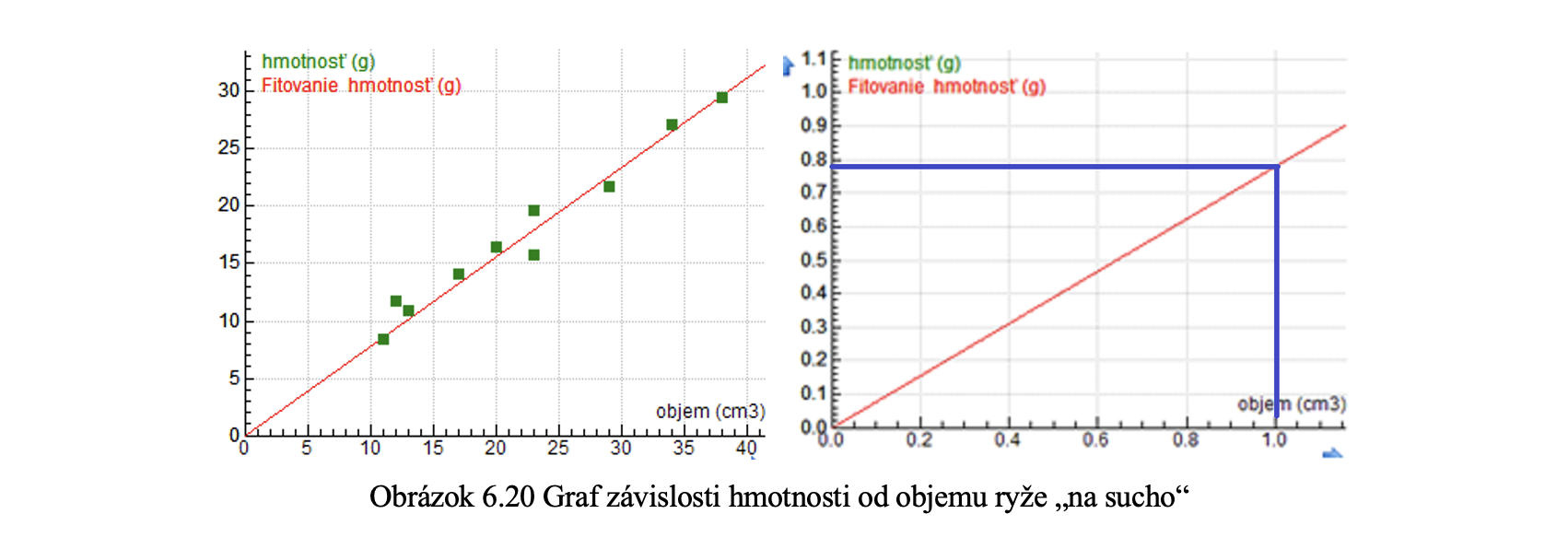    Z analýzy grafu žiaci zistia, že hustota ryže je menšia ako 1 g/cm3 . Výsledok je v rozpore s predpokladom. Avšak nie je možné hneď zamietnuť predpoklad. Je potrebné zamyslieť sa nad správnosťou predpokladu. Na základe získanej vedomosti a nameraných výsledkov by mala ryža plávať na hladine vody, ale skúsenosť je iná. Zrejme chybu musíme hľadať inde. Je správny postup určovania hustoty ryže? Je správna metóda určovania hmotnosti a objemu ryže? Žiaci zrejme objavia chybu vo svojich meraniach objemu ryže „na sucho“ – medzi zrniečkami ryže sa nachádza vzduch. Meraním objemu „na sucho“ zmerali aj objem vzduchu v priestore medzi zrniečkami ryže. Preto je potrebné zmerať objem zrniečok ryže znova spôsobom, akým sa meria objem tuhých telies (Lapitková, 2010, s. 60). Po opätovnom nameraní hodnôt a zostrojení grafu závislosti hmotnosti od objemu ryže „na mokro“ (obrázok 6.21), hustota ryže vychádza väčšia ako 1 g/cm3 . Tento záver je v súlade s naším predpokladom a aj so skúsenosťou, ktorú v tomto smere máme.
           
                


Pracovný list: Aká je hustota ryže?
    Ryža, ktorú konzumujeme, je plodom rastliny ryža siata. Z fyzikálneho hľadiska sa na ryžu môžeme pozerať ako na tuhé teleso. Tak ako každé teleso, aj ryžu (ako tuhú látku) môžeme charakterizovať veličinou hustota. Akú hodnotu má hustota látky, z ktorej je ryža? Je táto hustota väčšia ako hustota vody alebo menšia? V nasledujúcej aktivite hustotu látky, z ktorej je ryža určíme meraním.
Cieľ merania:
Zostroj graf závislosti hmotnosti od objemu pre telesá z homogénnej látky (ryže). Urč hustotu telesa odčítaním informácie z grafu.
Pred meraním:
Vyslov predpoklad o hustote ryže:
Hustota ryže bude väčšia – menšia – rovná* ako 1 g/cm3. (* Čo sa nehodí, prečiarkni.)
Pomôcky:
ryža, váhy (digitálne s presnosťou na 0,1 g), odmerný valec, ceruzka, pravítko.
Postup merania:
    1.	Do odmerného valca, ktorý máš k dispozícii, nasyp ryžu tak, aby si vedel určiť jej objem.
    2.	Ryžu z odmerného valca nasyp na misky váh. Urči hmotnosť ryže.
    3.	Zozbieraj údaje [objem, hmotnosť] ryže od všetkých skupín pracujúcich v triede a zapíš si ich do tabuľky 6.5 (tabuľku si môžeš vytvoriť aj v programe COACH).

Tabuľka 6.5 Namerané hodnoty hmotnosti a objemu ryže


                

Analýza merania:
    1.	Na grafe závislosti hmotnosti od objemu ryže prelož cez zobrazené body priamku.
    2.	Z grafu zisti, aká hmotnosť zodpovedá 1 cm3 ryže.
Odpovedz:
    1.	Z grafu urči, aká je hmotnosť ryže s objemom 1 cm3.
    2.	Z grafu urči, aká je hustota ryže.
    3.	Výpočtom zisti, aká je priemerná hustota ryže.
    4.	Zhoduje sa tvoj predpoklad s hodnotou hustoty určenou grafickou metódou?
    5.	Zhoduje sa tvoj predpoklad s hodnotou hustoty ryže určenou výpočtom?
    6.	Do misky nasyp ryžu a zalej ju vodou. Ako sa správa ryža vo vode? Čo môžeme povedať o hustote ryže v porovnaní s hustotu vody na základe tohto pokusu?
    7.	Bol tvoj predpoklad o hustote ryže správny? Svoje tvrdenie odôvodni.

Zmena v postupe riešenia:
Postup merania:
    1.	Na misku váh nasyp určité množstvo ryže. Urči jej hmotnosť.
    2.	Do odmerného valca, ktorý máš k dispozícii, nalej vodu tak, aby si vedel určiť jej objem Vvoda.
    3.	Ryžu presyp do odmerného valca s vodou a urči objem vody a ryže Vvoda+ryža.
    4.	Urč objem ryže Vvoda+ryža - Vvoda.
    5.	Do tabuľky zapíš hodnoty dvojíc objem a hmotnosť ryže od všetkých skupín pracujúcich v triede (tabuľku si môžeš vytvoriť aj v programe COACH).
Analýza merania: 
    1.	Na grafe závislosti hmotnosti od objemu ryže prelož cez zobrazené body priamku.
    2.	Z grafu zisti, aká hmotnosť zodpovedá 1 cm3 ryže.
Odpovedz:
    1.	Z grafu urči, aká je hmotnosť ryže s objemom 1 cm3.
    2.	Z grafu urči, aká je hustota ryže.
    3.	Výpočtom zisti, aká je priemerná hustota ryže.
    4.	Zhoduje sa tvoj predpoklad s hodnotou hustoty určenou grafickou metódou?
    5.	Zhoduje sa tvoj predpoklad s hodnotou hustoty ryže určenou výpočtom?
    6.	Bol tvoj predpoklad o hustote ryže správny? Svoje tvrdenie odôvodni.


Záver: